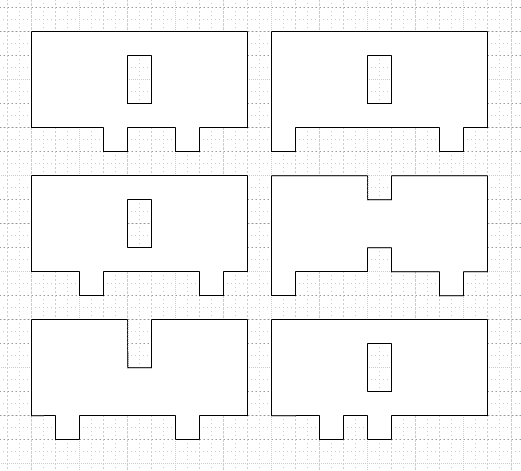Pavel's Puzzle Blog

As I've described elsewhere, I've taken to creating personalized puzzles for my young niece and nephew on their birthdays and at Christmas. The first puzzle I designed for my niece was for her fourth birthday. Of course, I tried to take it easy on her: no multi-stage complications, no difficult mechanical gyrations, and no Japanese logic grids. It was just a simple little 36-piece jigsaw puzzle of a photograph showing her and her brother smiling together. (As those of you who are parents already know, 36 pieces is too many for a four-year-old, but she had fun anyway, putting it together with the help of the rest of her family.)

Making that first jigsaw, though, made a lasting impression on me: I really enjoyed laying out all of the piece boundaries, trying to break up (or avoid breaking up) color regions, and looking for a clean, balanced distribution of cuts. Later that year, when I made another jigsaw for her brother for Christmas (that later inspired my puzzle Trail and Error), I got another jolt of that jigsaw-making magic sauce, and then I was well and truly hooked.

With several more jigsaws under my belt, I'm now ready to take the next step: offering to make a custom jigsaw puzzle just for you!

My jigsaws are laser-etched and laser-cut from heavy, 3/16" acrylic, giving them a sturdy, high-quality construction that means they'll stand up to lots of handling and remain crisp and clean for many, many years. Because they're etched, not printed, the design absolutely won't rub off or fade. It also means, though, that I can't do full-color imagery; the acrylic sheet will be one color and the etched areas will be whitened more or less based on the intensity of the laser. What that means, essentially, is that I can reproduce black-and-white photographs, line art, woodcuts, and other such monochrome designs. The highest contrast comes from using black acrylic, but many other bright colors can work well, too.

I can vary the number and the size of the pieces to your taste, from as few as a dozen pieces, say for a young child, up to a few hundred pieces, if you're looking for something more epic. Similarly, the difficulty of the puzzle is up to you: if you like, I can turn out a really nasty set of cuts and an irregular outside edge that should satisfy the most demanding of solvers, or I can give you a pleasant half hour of solving with a few friends. It's up to you!

One of my favorite things to design into a jigsaw is 'specials', pieces in representational shapes that either reflect the subject matter of the imagery or refer to the personality or history of the intended recipient. For example, as seen to the right, in a puzzle celebrating the release of Rachel Hartman's novel Seraphina, I included several musical instruments (reflecting a major theme of the book), Rachel's initials (traced from her own calligraphy on an earlier book cover), and the profiles of two characters from a comic book that Rachel had produced many years earlier. The specials can be whatever shapes you like, whatever it takes to make your custom puzzle truly 'special' to you!

Of course, the cost of a custom puzzle like this is going to vary a lot, depending on just what you're asking me to produce, but here are a few starting points to give you a sense of things:

• about 20 large pieces, including the letters of your child's name in a contrasting color, about 11 inches square, where the design is a simple maze of birthday balloons spelling out "Happy Birthday": $75
• about 40 pieces, 11 inches square, black and white photograph or other monochrome design provided by you, no 'special' pieces: $75
• same puzzle with four custom 'special' pieces: $115
• about 100 pieces, 11 by 18 inches, eight 'special' pieces: $200
• same puzzle, with about 200 pieces and 12 'special' pieces: $350

In all cases, these prices are for the first copy. If you'd like multiple copies of exactly the same design, the additional copies would be $30 to $60 each, depending on the size and number of pieces.

Does this sound intriguing to you? Wouldn't this make a great birthday or holiday present, or maybe a unique promotional item for your business? Please get in touch with me at pavel@pavelspuzzles.com and let's start talking about how I can make a very special puzzle, just for you!

Posted by Pavel at 04:03 PM | Permalink | Comments (0)

Many years ago, while visiting some friends in Port Townsend, Washington, I came across a very unusual disassemblable sculpture, made from about 9 or 10 pieces of bronze. Each piece looked like a molten metal droplet, conforming to the shapes of the pieces underneath it. It looked like the maker had dropped a bit of molten bronze into a small cylinder, let that cool, then dropped another molten bit partially on top of that one, let it cool again, and then repeated this process, droplet by droplet, until he'd built up a little tower of droplets inside the cylinder. By some alchemical magic, none of the droplets had stuck to the cylinder or to each other, so you could lift off each droplet again in turn, effectively reversing the process of its creation.

As a sculpture, it was fascinating, and as a puzzle, it was wonderful. Each time you added a piece to the growing tower, it locked itself into place with an incredibly satisfying 'click'. It was an addicting combination: heavy, organic, natural shapes that felt great in your hands, then interlocking and conforming to one another so tightly as you assembled them together. Obviously, I bought the one they had there in the shop. (I can't seem to lay my hands on that puzzle just now to take a photo of it, but you can see a few other examples here and here.)

Several years later, I spent some time tracking down the maker, calling every gift shop in Port Townsend until one recognized my description of the sculpture and put me in touch with Steve Johnson, the owner of a metal foundry there who'd created and sold the sculptures under the brand name Paracelsus Puzzles. You may have noticed that I used the past tense there. I discovered in my conversation with Steve that he'd long since stopped making the puzzles and gone back to normal metal-foundry work; puzzle people had apparently proven too demanding, always asking for new designs, and he'd eventually just gotten tired of it. Worse, he'd never revealed or licensed his magical don't-stick technique to anyone, so nobody else could make them either!

I was disappointed, of course, but it occurred to me that I was living in the Puget Sound area, the land of Dale Chihuly and the Glass Museum. There are tons of great glass artisans around the greater Seattle region; surely I could convince one of them to work with me to replicate something of the feel of those metal puzzles in heavy art glass! Sadly, though, every time I brought up the idea with glassblowers, here and elsewhere, they looked at me like I was crazy, or at least naïve. They would always patiently explain that, if you get glass hot enough to melt and run like that, there isn't anything you can do to keep it from sticking to any other glass it touches. After a while, I gave up on my little dream and stopped asking.

Several years ago, though, my wife and I were driving down the Oregon coast, and we stopped in to visit an old college friend of mine, Sarah Gage-Hunt, whom I hadn't seen for some 25 years. I discovered that, in addition to teaching high-school math, she had become a fused-glass artist, heating carefully arranged bits of glass in a kiln to melt them together into beautiful dishes, platters, and sculptures. I couldn't resist bringing up the puzzle-sculpture idea, just one more time, and to my delighted surprise she said, "Oh, sure. We can do that. No problem." After I got over my shock, we spent pretty much the rest of our visit talking about techniques and sculpture ideas, until our respective spouses got thoroughly tired of it and made us stop.

It took us a while to refine our ideas and techniques, but we finally got something worth offering to you, the puzzle-buying public: we call it Dali Bottles. Each sculpture is made from about a dozen real beer bottles, plucked from certain doom in the recycling bin. We first melt each bottle separately in the kiln overnight, flattening it like all of the air has gone out of it. Then we stack all of the bottles up in a random, circular or square arrangement and run that though the kiln one final time. The bottles in the stack slump over and hang on one another like the watches in that famous Salvador Dali painting, each conforming so tightly to the ones beneath it that there's literally no space left at all. When you're putting the stack back together, you will have no doubt whatsoever when you get one into the correct position: it 'clicks' into place so strongly, so surprisingly, and just so satisfyingly that you'll find it impossible not to smile. Really, folks: I cannot convey to you clearly enough how truly wonderful that feels.

As I said above, it's been several years since Sarah and I started this project and, in the meantime, Sarah has retired from teaching and moved onto a sailboat in the Caribbean. No, really! There's no room on the boat for her kiln, so she kindly sold it to me, and now it lives in my garage. However, I haven't yet put in the dedicated electrical circuit necessary to run it, nor gotten up to speed on making Dali Bottles myself.

The upshot is that, for now, we only have available those sculptures / puzzles that Sarah made before she retired. Take a look at photos of all of the sets we have on hand and then select the one you'd like from the menu below.

Posted by Pavel at 05:50 PM | Permalink | Comments (0)

One great thing about being an uncle, as opposed to a parent, is that you have a societally acknowledged right to spoil your nieces and nephews. Personally, I take that right a step further: I believe that it is my obligation to fill in any holes I see in the rearing environment provided by my sister and her spouse for their children. Specifically, I see it as my role to corrup—I mean, indoctrinate—my niece and nephew into the world of puzzles.

(Admit it: you're surprised, aren't you? No? Oh, well, never mind that then.)

I think I started in on my nephew when he was only eight or nine years old, making a couple of small pencil-and-paper puzzles for his birthday that led to some kind of a silly metapuzzle answer. For his tenth birthday, I stepped it up a bit to a sequence of four puzzles, each unlocking the next, leading to him finding his real present, hidden somewhere around his house. He's 11½ as I type this, and I'm already planning something even more involved for his twelfth...

I tell you all of this because my nephew was the original inspiration for this puzzle. For his Christmas present last year, I wanted to try my hand at creating a jigsaw puzzle. Of course, I couldn't just leave it at that, could I? No, I had to make it one of my multi-stage puzzles: after he'd solved the jigsaw, there would be a new puzzle revealed, and that would lead to yet another puzzle, until he finally got a satisfying answer. The version I made for him led to a final message that was very silly indeed, and very specific to him; it was his present, after all.

After Christmas, though, I got to thinking that the main ideas in his puzzle were good enough that I should really use them again in a puzzle for the website. Some months later, I finally got around to creating the puzzle you see here, and testing has shown that it works pretty well. It's a real jigsaw puzzle, and not a trivial one, but also not a huge one; it's only 64 pieces, but take my word for it: it'll still keep you busy for a little while. And, of course, that's just the beginning of the solving experience! I won't even tell you how many layers of additional puzzle there are after assembling the jigsaw; not only would it spoil some of the surprise, but it's actually a little tricky to count them!

(By the way, the puzzle's name isn't a typo; believe me, you'll understand why by the time you finish this one...)

So the question comes down to this: my 10½-year-old nephew handily solved his version of this puzzle; can you do as well with yours?

Posted by Pavel at 10:25 PM | Permalink | Comments (0)

This Spring, I once again attended the Gathering for Gardner, that eclectic (or is that eccentric?) conference bringing together mathematicians, puzzlers, and stage magicians for talks, conversation, demonstrations, and fun. One thing that particularly caught my eye this year was a large, beautiful, wooden tray puzzle that the mathematician and writer Barry Cipra was showing off. You can see my snapshot of it to the right.

As any good mason knows, when you're laying courses of bricks, you want to avoid having the cracks between bricks in one row lining up with the cracks in other rows: aligned cracks tend to make the wall weaker. This puzzle puts you in the role of a bricklayer with very high standards indeed: you must arrange the bricks such that no crack in one row lines up with a crack in any other row!

After playing with Barry's puzzle for a little while, I knew that I wanted to make my own version of it.

Then, to give the solving experience a little more texture, I wrote some software to help me craft a set of increasingly difficult challenges. The first is just to lay out the pieces as I described above, and there are 2,184 solutions to that. The next challenge is to find a solution that has 180° symmetry, one where the solution looks the same after you turn it upside down (other than the colors, of course); there are only 56 solutions to that one. The third challenge is to ignore that symmetry idea and, instead, to find a solution where no two pieces of the same size (4 units or less) overlap each other vertically; that takes us down to just 5 solutions. Finally, you have to find a solution that obeys both of those last two constraints: 180° symmetry and no same-size overlaps. That final challenge has (wait for it...) exactly one solution.

What I particularly like about this puzzle is that it spans a nice range of difficulty: the first challenge should yield to anyone who puts any patience into it, but solving all four challenges should keep most solvers busy for a nice little while...

Posted by Pavel at 10:13 PM | Permalink | Comments (0)

One of my best-selling puzzles is the Finnish Cross (formerly known as Six Tabbed Planks), designed by Matti Linkola. That might be simply because it's one of the least expensive puzzles on the website, but I prefer to think that it's because it has a compact elegance about it that makes it fit well on a executive's desk or anywhere else. I have received one or two letters about it, though, from purchasers who were disappointed at its overall size (about two inches cubed).

In its pure form, though, the puzzle has a certain fixed aspect ratio: if I made one twice as large, it would necessarily be made from plastic that was twice as thick (1/2 inch instead of 1/4 inch). It's a slow and tedious process to laser cut such thick acrylic, and some artifacts of the cutting process get magnified as well.

For example, the laser doesn't cut a channel that's at a perfect right angle to the surface; the channel is more V-shaped, wider on the 'entry' side and narrower on the 'exit' side, so the pieces end up being slightly trapezoidal in cross section rather than rectangular. Now, proper laser-cutting technique can significantly mitigate such tendencies, but as you scale up to thicker and thicker materials, the artifacts start to overwhelm the mitigations. For a 3D interlocking puzzle like the Finnish Cross, the result wouldn't be as satisfying as I'd like.

One morning, as I pondered this 'size matters' issue, I idly noted that I had managed to build up a small inventory of fluorescent blue acrylic, originally intended for use on a commission where we ended up going in a different direction. That plastic had always put me in mind of the shockingly blue ice we'd seen on Alaskan glaciers, and now that led me to picture a version of the Finnish Cross that looked like a whole bunch of icicles had been jammed together into a kind of starry, snowflakey shape. The idea really appealed to me, and I immediately sat down with my drawing software. A few hours of design later, I was ready to try cutting out the first prototype for Icicle Jam, and the result was just as striking as I'd imagined.

This jagged, icy beauty is big, about 6-1/2 inches in diameter, and really eye-catching in any setting. The internal interlocking configuration is the same as in the Finnish Cross, but I find it's a little bit tougher to visualize it in this new, more flamboyant form, making for a slightly more difficult solving experience. If you're looking for a satisfying puzzle that will really remind you of its sub-Arctic roots, Icicle Jam may be just the ticket!

Posted by Pavel at 03:37 PM | Permalink | Comments (2)

In the summer of 2009, at the annual International Puzzle Party, we were treated to a talk by the justly renowned computer scientist, mathematician, and author (and all-around Really Nice Guy™) Donald Knuth. He spoke about some of his favorite puzzles and some new puzzle ideas he'd been working on. As part of the presentation, he passed out a sheet of paper with several puzzles on it for us to solve later.

One of the entries on the paper was a description of an interesting set of twelve trominoes (aka triominoes), pieces made up of three unit squares joined in a little 'L' shape. Each piece had a line drawn on it (on both sides, so you could flip the pieces over), and your goal was to arrange them into a six-by-six square such that all of the lines formed a single, unbroken loop The solution, he said, was unique. OK, fun enough, but Don wasn't through, not by a long shot.

Then, he listed four more similar trominoes and said that, if you added those new pieces to the original ones, you could arrange them all into an eight-by-six rectangle, with the lines again forming a single continuous loop, and again the solution was unique. This was sounding even better, but he kept going!

Next, Don showed two more trominoes to add in, now enabling you to build a unique nine-by-six rectangle with the same properties. That was followed by yet two more trominoes, now forming a unique ten-by-six rectangle!

Finally, he showed four more tominoes you could add to everything that had gone before, with the entire set now making a nine-by-eight rectangle, still with the lines forming a single continuous loop, and still with a unique solution!

Five separate, progressively more difficult challenges, all from the same set of simple-seeming pieces, all with unique solutions: this was great, an elegant puzzle construction! There was only one teensy-tiny little problem: Don hadn't actually given us the puzzle! All we had was a description of the puzzle, stuck on this sheet of paper!

I immediately resolved to design a nice physical packaging of Don's puzzle idea, with all five challenges and all twenty-four tromino pieces included, along with a simple way to remember which pieces went with each challenge. The result is Tromino Trails. The initial six-by-six challenge isn't trivial, but also isn't particularly difficult. After that, each challenge poses a progressively tougher problem but also trains you, in a sense, to be ready for the challenge that follows.

My friend Stan Isaacs used this as his Exchange puzzle at this summer's International Puzzle Party in Berlin, and now I can make it available more broadly. I think it provides a very satisfying puzzle experience that's accessible to and enjoyable by both experts and new puzzlers alike.

Posted by Pavel at 02:43 PM | Permalink | Comments (0)

A couple of years ago, I was privileged to be commissioned to produce a unique, custom puzzle for the 2009 Science Foo Camp, a eclectic annual gathering of scientists sponsored by the journal Nature, by Google, and by O'Reilly Media. I ended up producing 300 copies of a special version of my then-new puzzle Anansi's Maze, which they then handed out to all of the attendees that summer. I was also invited to attend the event myself, which was truly wonderful, and they asked me back again the next summer. At the event in 2010, I started discussing with the organizers the possibility of my producing another puzzle for them for the 2011 gathering, this time a puzzle that had been designed from the beginning specifically with that event in mind.

I spent some time brainstorming puzzle themes with Kay Thaney from Nature, and we hit upon what I thought was a great inspiration. Tim O'Reilly, the founder of O'Reilly Media and one of the organizers of the event, has a favorite saying that he brings up at the introductory session of each Foo Camp:

When Tim says this, he's referring to the edges between intellectual disciplines, and how Foo Camp is designed to bring together people from different areas and enable a kind of creative friction as the areas butt up against one another.

When we brought up the saying in our puzzle-theme brainstorming, however, it immediately took on an entirely different meaning for me, and my mind began chewing over all sorts of ideas for embodying that meaning in a puzzle design. Edgewise is the result of that chewing. (Hm. That sounded better in my head than it reads here. Oh, well...)

Edgewise consists of about two dozen jigsaw-puzzle pieces, most with large letters etched on them, and some with additional words of potential significance. As this is the latest in my series of multi-stage puzzles, I won't say anything more about the solving experience here, but I can tell you that it should keep you happily busy for a little while as you make your way through it.

In the end, ironically, Edgewise did not wind up being used as a Science Foo Camp gift, but I remain grateful to Tim and Kay for providing the inspiration for this puzzle. We did use it in this summer's Microsoft Intern Puzzleday event, and I also used it for my Exchange puzzle at the International Puzzle Party in Berlin, so I think it's getting the kind of exposure it deserves, particularly because now it's available here on the website for you to try out for yourself!

Posted by Pavel at 02:43 PM | Permalink | Comments (0)

Even before I began designing my Anansi's Maze puzzle, I'd been thinking about how to create puzzles that intrinsically relied on the transparency of the pieces. My inspiration was a relatively unusual and little-known sub-genre of mechanical puzzles, sometimes called overlapping puzzles, in which the pieces have openings or transparent sections and your goal is to find a way to stack up those pieces and form a picture from the intersection of their transparent bits. The first puzzle I know of in this family was released way back in 1900, but there's been a steady trickle of examples ever since.

I got one such in the Puzzle Exchange at one of my first International Puzzle Parties. It consists of six octagonal pieces of transparent acetate, each laser-printed with a gray-scale image; if you stack up the pieces just right, the gray bits combine and darken and you end up with quite a nice picture of a dog, if I recall correctly. Mostly, I remember it being really difficult.

Still, the notion had stuck with me. I wanted to play in that design space, but I also wanted to make a puzzle that wasn't so tough to solve. I had the idea that I could make it easier by sharply reducing the number of layers, maybe using only two or three. To keep it from becoming trivial, I could break each layer into multiple pieces, so that you'd have to assemble the layers themselves before you could stack them up.

So far, so good, but then I got ambitious: what if you could assemble the layers in more than one way? What if you could form either of two different pictures from the same pieces, depending on which assembly you built? This whole story got me pretty excited: this could be a really cool puzzle! Now I just needed to actually design such a thing...

And there the idea sat, more-or-less unmoving, for almost two years.

The problem was, I had no idea how to go about creating this kind of a puzzle. Unlike many of my designs, I couldn't see any way to write software to help me search for a puzzle that would match my story; one of my key design tools had been stripped away from me!

I finally picked up the idea again late last winter, when I was trying to come up with a new mechanical puzzle for use in this summer's Microsoft Intern Puzzleday. There wasn't anything magical about the process, I just dug in, started drawing potential pictures, overlapping them, and looking for interesting area intersections. It was a very incremental, iterative design journey, one of the most difficult puzzle-design efforts I've been through. Even after I'd finished the artwork, what I'd thought of as the hard part of the process, the design went through five different prototype and test-solving iterations before I finally hit on the right combination of cleverness, accessibility, and clarity of solution.

In the end, ironically, the puzzle was completed too late to be used in Puzzleday, but I did use it as my Exchange at IPP 30 in Osaka later this past summer. I had barely enough copies made then to satisfy the Exchange rules, with just a few left over at the time for selling. By the time I finished with building those, I knew that I wanted to do yet one more, fairly minor design iteration before putting the puzzle up here on the website. What with one thing or another, it's taken me a while to do that iteration, but now it's done, and I'm quite happy with how the puzzle has turned out. I hope you'll enjoy it too!

Posted by Pavel at 10:42 PM | Permalink | Comments (0)

As I've described before, there's a marvelous biennial conference in honor of Martin Gardner called, appropriately enough, the Gathering for Gardner. It brings together three communities that Martin was active in, and in which Martin was very influential: mathematicians, puzzle people, and stage magicians.

No, really.

Each conference has a theme, and that theme is the sequence number of that conference. My first Gathering was the eighth one, so its theme was the number 8. (Did I mention the mathematician connection?) Anyway, everyone who comes to the conference is supposed to bring something for everybody else, all 300 or so of us, and ideally it will be something related to the theme number. I thought I was pretty clever when I came up with a very eight-related puzzle to give everyone.

My friend Bob Hearn, though, took literal-mindedness to a whole new level: he designed and gave out a puzzle that was entirely built out of the word "EIGHT". He found a clever style in which to draw the letters in "EIGHT" so that there are lots and lots of ways to neatly link those letters together, and then he picked a particularly cute couple of those ways and turned each one into a tray-packing puzzle.

The "Easy Eight" side of the tray appears perfectly straightforward, just a simple square. The problem is that it's kind of tricky to figure out how to get all five letters to lie flat in there at the same time: so many cute ways to fit the letters together, only one way to actually pack them into the tray.

Bob couldn't just leave it at that, though. No, it wasn't enough for him to create a really clever and elegant puzzle. He had to do it twice, with the same set of pieces. The (unique) solution to the "Hard Eight" side of the tray is equally clever, and equally elegant, and awfully tricky to find! It probably never occurred to you before, but an ellipse doesn't have any corners. None at all. There's no obvious way to start on this side, no clear surety that you're making any progress at all until, suddenly, there it is: the pieces are really, really close to fitting in. A little more tweaking, some tiny adjustments, and then you realize you're still not putting them in correctly!

Ahem. Sorry, got a little carried away there. Just a little puzzle-frustration flashback. I'm fine now.

As soon as I finally solved both of Bob's lovely Eights, I started talking with him about offering a version of his puzzle on this website. It's taken me a long time to pull it together (the tolerances for the "Hard Eight" side are pretty tight), but I've finally succeeded, and now I can make this wonderful creation available to you. This is a puzzle you'll enjoy solving yourself, and then really enjoy torturing your friends with. Really, what more could you ask?

Update: Easy Eight / Hard Eight is now also available in this economical CD jewel-case edition! (Note: your tray and piece colors are likely to differ from what's shown in this photo. We use a wide variety of colors and every puzzle is made from a different pleasing assortment.)

Posted by Pavel at 10:03 PM | Permalink | Comments (0)

In March of 1931, a man named Theodore Edison, younger son of the famous inventor Thomas Alva Edison, filed articles of incorporation for a company named Calibron Products in West Orange, New Jersey. The company's first product was a special kind of graph paper, designed to make it easier to create perspective drawings.

But in December of the next year, the company filed for a copyright on "The Calibron 12-Block Puzzle". An advertisement for the puzzle appeared a few years later, in the January 1935 issue of Popular Science magazine.

The instructions for the puzzle read, in part, "The problem is to arrange the twelve blocks to form a single large rectangle. Any rectangle will do, provided that all twelve blocks are used... We guarantee that there is a straightforward, accurate solution of this puzzle in a single plane, and without recourse to any kind of trick... However, in spite of the enormous number of possibilities, there appears to be only one basic arrangement which satisfies the above conditions... We once offered $25 for the first solution of this problem and distributed hundreds of puzzles at that time, but received almost no correct arrangements! We should like to hear from you if you succeed in making the rectangle unaided."

Not very many people have copies of the original Calibron 12-Block Puzzle, and that bothered a good customer of mine, who wrote me earlier this year asking for advice on how to get a few copies of the puzzle made. I decided to make the copies for him myself, and once the first prototype came off the laser cutter, I decided that it was quite an intriguing design, and that I'd like to make it more widely available again.

The twelve rectangles making up the puzzle have very promising dimensions, with lots of obvious interrelationships that lead you to think that won't have too much trouble getting them to fit together in nice ways, and that's true, as far as it goes. However, "as far as it goes" isn't likely to be as far as actually solving the puzzle unless you put in some time and concentration. This is one of those very attractive puzzles that just won't yield without a bit of a fight.

With modern computers, it was straightforward to verify the original marketing claim: there is, indeed, a unique solution to the puzzle. I think you'll enjoy torturing your friends as they try to find it.

Posted by Pavel at 05:25 PM | Permalink | Comments (0)

Take a 2x2 square, and join it to another 2x2 square, but only by half an edge. There's only one way to do that (ignoring reflections and rotations), shown below:

Back in 2002, my good friend Derrick Schneider noticed this nice little set of slightly strange shapes and wondered whether or not they'd make a good puzzle. He whipped up a little program to try packing the pieces into an 8x8 tray. To his delight (and later ours), there was just one way to fit in all four pieces! Many designers would have stopped there, but for some reason Derrick also tried running the program on a 7x9 rectangle: once again, incredibly, there was a unique solution!

Imagine the fun: he comes up with a simple way to define a set of pieces, the resulting set is nice and small, and that set fills both of the two most obvious tray shapes in unique ways. Believe me, such a mathematically elegant puzzle design doesn't come about every day! Add to that, the resulting puzzle falls into a real sweet spot of difficulty: harder than you might guess (those pieces are just plain tricky to get your brain around, especially the curled-up one), but easy enough to yield to a little patience.

Perhaps that explains why, when Derrick presented his puzzle at the 22nd annual International Puzzle Party, the jury for the Puzzle Design Competition awarded it an Honorable Mention, one of just three puzzles so honored.

Now, for the first time in many years, I'm happy to make Derrick's wonderful little puzzle available for sale again. Initially, I'll be selling off the remainder of Derrick's original manufacturing run; the last time I visited, I got him to dig around in the basement and pull out all of his old inventory for me. After that limited supply sells out (he could only find about 15 of them), I'll start making my own copies for you. This is simply too good a puzzle to remain unavailable for so long.

Update: Square Dance is now also available in this economical CD jewel-case edition! (Note: your tray and piece colors are likely to differ from what's shown in this photo. We use a wide variety of colors and every puzzle is made from a different pleasing assortment.)

Posted by Pavel at 04:25 PM | Permalink | Comments (0)

As I write this, I'm helping to host the first Microsoft Non-Intern Puzzleday, a re-run of the puzzles from this year's regular Intern Puzzleday, just to give the actual Microsoft employees a whack at them. I'm sitting outside a room in which I've set up six "solving stations" for the multi-stage mechanical puzzle I contributed this year, Anansi's Maze. (The Intern Puzzleday actually has a budget, so I could afford to give each team a copy of the puzzle; for the non-interns, they have to timeshare.)

This year, I wanted to play with transparency, as you could probably guess from the picture. I started out with a much more complex puzzle idea, but whittled it down, stage by stage, to get something that was a more appropriate level of difficulty and that hung together more completely. The result, I think, is my best multi-stage puzzle yet, so I decided to also use it for my 2009 Exchange puzzle at the International Puzzle Party in San Francisco.

Anansi the Spider is the trickster spirit of Caribbean and Western African myth and legend, known for his creative mischief making. This puzzle will tease you with its ambiguities and lead you on a merry chase to find its hidden meaning.

Here is a maze, Anansi tells us, but there are no walls, no paths to follow, let alone any dead ends or cycles. Our treasured ‘right-hand rule’ is useless in these uncharted territories.

Anansi’s Maze is a multi-stage solving experience: finding the solution to one stage leads to a new puzzle, and that one to another! Where does this pathless path lead? Can you see through all of Anansi’s tricks and find the answer he’s left for you at the end of your journey?

Posted by Pavel at 06:32 PM | Permalink | Comments (0)

Last year, my puzzle-design mind kept drifting to polyhedra, specifically to ways for pieces representing the faces of polyhedra to connect and interact with one another at each edge. My Octamaze and Gamesters of Triskelion puzzles came out of this realm, and for my IPP 2008 Exchange puzzle, I wanted to move up from the octahedron to my favorite of the Platonic solids, the dodecahedron. My experience with the tab-and-slot mechanism of the earlier puzzles, though, had made me very dubious that such an approach would continue to work for the rather larger dihedral angle of the dodecahedron: the tab would be coming into the slot at such a shallow angle that the slot would have to be quite wide, and the piece deformation needed to insert the last face probably wouldn't work at all, let alone elegantly.

I also wanted to use a prettier material than the opaque black high-impact polystyrene I'd used before, and that ruled out pretty much any piece deformation at all. (I'd tried making Octamaze out of acrylic, since it takes etching much better than polystyrene does, but after having my acrylic prototype shatter in my hands during disassembly, I gave up and went with the much more robust and pliant polystyrene.)

I decided that the pieces would rotate into position, using some kind of interlocking, hook-shaped protrusions on the edges of each face; that would still entail fairly wide (deep?) hooks, due to the shallow angle, but avoid any piece deformation during assembly. I realized that I might run into a mechanical problem with the corners of the faces hanging up on one another as each face was rotated into position, so I started considering various piece shapes that were missing the face corners. I started playing around with actual shapes on paper, instead of just thinking about all of it, and all of this came together in a kind of practical lesson in geometric duality: the hooks would be on the ends of arms, and the puzzle would look like stars with interacting points rather than the regular polygonal faces I'd originally imagined.

The resulting puzzle is probably the prettiest one I've ever designed, once assembled: it would make a great Christmas ornament, or an attractive object to dangle from the rear-view mirror of your car, let alone just sitting on your desk at work. It's also quite a difficult puzzle, so keep that in mind if you buy a copy. Like all of my puzzles, it comes with the solution, though, so nobody need know if you decide to short-circuit the solving and jump to the pretty bit.

[Update 8/27/2011: I've renamed this puzzle to "Crystal Ball", which I think describes it better than the old name, not to mention avoiding potential trademark issues... :-)]

Posted by Pavel at 05:21 PM | Permalink | Comments (3)

My orignal plan, when designing the Octamaze puzzle, was that it would serve double duty, being both my gift to everyone at Gathering for Gardner 8 and something to torture the interns with at the 2008 Microsoft Intern Puzzleday. Sadly, though, it became quite clear during initial playtesting that Octamaze would be too difficult for the intern event. (I was willing to make the mathematicians, puzzlers, and magicians at G4G8 work harder...)

Still, I thought I could at least reuse the primary mechanical idea of Octamaze, and so I started from there when designing the Gamesters of Triskelion puzzle; I did, though, make that part a bit easier. The 2008 Puzzleday theme, for those of you who didn't recognize it immediately from the title, was Space, including many science-fiction references. I was put in mind of the Gamesters of Triskelion episode from the original Star Trek series by the triangular shape of the pieces from Octamaze, and somehow it occurred to me to check whether or not "triskelion" was actually a normal English word. As it happens, it is: a triskelion is a (sometimes quite literally) three-legged motif from heraldry and graphic design. I particularly liked some of the more modern interpretations of the motif, so I incorporated one into the etching on the pieces.

Gamesters of Triskelion is the third in my series of multi-stage puzzles, where solving one stage of the puzzle creates another puzzle for you to solve, on through some number of stages until you reach a single-word or short-phrase final answer. I'm having a lot of fun designing such puzzles, so you can expect the series to continue for quite a while.

Unlike most of my puzzles, this one comes with some "flavor text", not essential to solving the puzzle, but perhaps helpful:

Captain's log, stardate 3211.9: We are leaving starsystem M-24 Alpha, having convinced the three disembodied Providers, the one-time Gamesters of Triskelion, to help their former gladiators to form a new, free civilization. This should end the deadly gambling in their obsessively triangular fighting arena.

As we left orbit, the Providers transported a small octahedron onto the bridge, along with an engraved tablet (three sided, of course) in what appears to be their language. During transport, the faces of the octahedron detached from one another, so now we have eight triangular pieces.

Spock believes it will be straightforward to reassemble them since, he says, they can only fit together in one way. He is more puzzled about the meaning of the etchings on the faces, and how they might relate to the tablet, but assumes that this will become clear once the octahedron is back together.

Posted by Pavel at 09:57 AM | Permalink | Comments (0)

Back in 1994, some folks decided it would be a cool idea to give a special 80th birthday present to Martin Gardner, long-time author of the very popular and significant Mathematical Games column in Scientific American magazine, as well as many books of mathematical puzzles and articles.

What better way to mark the occasion, they thought, than to bring together a lot of people who had enjoyed, and been influenced by, Martin's work? So they invited a bunch of people from the fields nearest to Martin's heart, from mathematics, puzzling, and stage magic, to come to Atlanta for the "Gathering for Gardner": several days of talks, performances, and exhibitions in celebration of Martin's 80th birthday. That first Gathering was such a huge success that the organizers decided to keep doing it and, every two years since then, there's been a Gathering.

I've known about the Gathering for some time now, through contacts at the International Puzzle Party, but I was pleased to be invited for the first time this year, for "Gathering for Gardner 8", or "G4G8". Similar to the Puzzle Exchange every year at IPP, the organizers of the Gathering ask that everyone provide a gift of some sort for all of the other participants. Many people fulfill this obligation by giving a talk and writing up a short article for the conference proceedings book, but many others bring puzzles, magic tricks, or other entertaining objects.

You know, of course, what I did, right?

Every Gathering for Gardner has a theme; I think you may be able to guess what all of the previous themes were when I tell you that this year's was "8, or the crazy lazy 8 (infinity)". I wanted to bring a new puzzle design that would strongly incorporate the theme, of course, but I also wanted to continue down the path I'd forged with my Ooo Tray puzzle last year. I wanted to design another multi-stage puzzle, with each solving stage revealing clues to the next stage, culminating in a "final answer" that was somehow satisfying.

I'd been idly thinking about three-dimensional edge-matching puzzles for a while (What? Don't try to tell me you don't think about such things, too.), and I'd wondered if it would work to make a polyhedron where the sides fit together with tabs and slots. With a theme like "8", this was a perfect (some might say Platonic) opportunity!

A little software work and many design iterations later, Octamaze was born. There are at least four stages in solving this puzzle, providing a good hour or two of "play time". If you buy a copy of Octamaze and get stuck, I've created a sequence of web pages giving a progression of hints for solving it. (Don't worry: clicking on that link won't immediately reveal any spoilers. If you keep clicking on the links at the bottom of each page, though, you'll eventually see all of Octamaze's secrets, so be careful.)

Posted by Pavel at 10:18 PM | Permalink | Comments (2)

I originally blogged about this puzzle a couple of years ago, shortly after I got my first copy of it, six years in the making. A few days after that, I got email from my friend George Miller, telling me that he'd laser-cut his own copy and liked it a lot. He showed that copy to long-time IPP attendee Stan Isaacs, who asked me for permission to use it in the IPP 26 Exchange, in Boston. At the time, I had a different puzzle in mind for my own exchange gift, so I agreed. Unfortunately, that other idea fell through (sometimes that happens with puzzle designs), so I ended up not exchanging that year. Instead, I was Stan's exchange assistant, which was fun in its own way.

The version that Stan exchanged was somewhat different from my original copy: he and George reshaped the pieces from rectangles to half circles, making the completed puzzle into a sphere instead of a cube; they called it the "Fan-Way Park Ball", following the Bostonian theme. They also used laser-cut maple instead of plastic and reduced the size to about 1-5/8 inches. It was cute in its own way, and I was happy to see the puzzle exchanged, but I still preferred the clear Lucite look of my original version; it looks a bit more stylish sitting on your desk.

I'm now happy to announce that I can offer copies of my version for sale here. The puzzle is shipped disassembled, flat, and putting it together provides a very satisfying but accessible solving experience.

[Update 8/27/2011: I've renamed this puzzle from "Six Tabbed Planks" to the more euphonious "Finnish Cross", in honor of its original designer, Matti Linkola. It's still the same great puzzle, just with a spiffy new name!]

[Update 4/9/2012: I now have The Finnish Cross available in three jewel-tone colors, in addition to the original crystal clear. Check it out!]

Posted by Pavel at 02:56 PM | Permalink | Comments (3)

Every year, a group of volunteers puts on a one-day puzzle event for Microsoft's summer interns here on the Redmond campus called Intern Puzzleday. It's kind of a scaled-down version of the more well-known (and ambitious) Microsoft Puzzlehunt events. Although Puzzlehunt traditionally begins at about 10am on Saturday and continues straight through to dinner time on Sunday, Intern Puzzleday is a kinder, gentler one-day affair, almost exactly 24 hours shorter than Puzzlehunt.

This year, I had the great fun of joining the team of volunteers putting on Puzzleday 2007, and I designed or co-designed five different puzzles for the event, three of which we finally used on the day itself. Perhaps I'll write a fuller description of the event later, but for now I'll just show one of the puzzles I designed for it.

Traditionally, Puzzlehunt and Puzzleday puzzles are designed to have a short, one- or two-word answer that solvers can type into email or a web page to prove that they've finished. All of those answers are later used in one or more layers of "meta-puzzles" leading eventually to a final "hunt" somewhere on campus for an artifact specific to that hunt's theme.

I wanted to find some way to incorporate a mechanical puzzle into this domain that's typically dominated by paper-and-pencil or on-site-event puzzles. To do so, I started with the tray and piece design from my "Perkinson Guest Bathroom Tile" puzzle and laser-engraved some additional information on both. The result is, I think, something new in the world of mechanical puzzles: a puzzle with an answer, not just a solution. In this case, the answer is just one word long, and finding it takes you through a multi-layer solving experience; guidance for the first layer is etched right onto the tray ("Place all twelve pieces flat in the tray"), and solving each layer reveals more guidance on how to attack the next one. There are a total of three or four layers to this seemingly simple puzzle, depending on how you count. During Puzzleday, the Ooo Tray was solved by all 28 teams of interns, and it was the first puzzle that many teams worked on.

Update:
I'm now making this puzzle in beautiful natural cherry! I've also tightened up the design slightly from the original to give the puzzle a somewhat nicer look and an even more satisfying ending.

Posted by Pavel at 07:57 PM | Permalink | Comments (0)

Flush with the successful design of the "Perkinson Guest Bathroom Tile" puzzle, the obvious next step was to consider dominoes instead of trominoes. This time, I allowed the pieces to be flipped over, and I also counted pieces whose two tiles had their tilted edges at right angles to each other. This leads to a complete set with 13 members, some of which are slightly strange looking, and one of which (with the two tilted edges joined together) is a quite boring perfect rectangle.

Leaving out the boring rectangle, we get twelve roughly one-by-two-unit dominoes; the obvious tray shape is a six-by-four-unit rectangle. Can the (nearly) complete set fill that tray? Sadly, my packing program said no, and this time it also didn't work to change the top and bottom edges into the angular "sine wave" pattern from the bathroom-tile puzzle. I had my local laser cutter, Joe Pelonio, make me up a set of the pieces anyway, so that I could play with them and try to get a feeling about why the rectangular tiling wouldn't work. The first thing I noticed when I got the pieces in my hands was that one of them looked a lot like the profile of one of the famous "moai" heads from Easter Island; thus the eventual name of the puzzle.

When I presented Easter Island Dominoes at the 2007 IPP Exchange in Australia, I told the following story:

It's not well known (especially to archaeologists), but many, many sets of these 12 pieces have been discovered in excavations on Easter Island. Never, though, have they come across a copy of that elusive 13th piece, the perfect rectangle. From this, we can infer that the ancient Easter Island culture, now long lost to us, did not approve of straight lines and perfect rectangles. Being a culturally sensitive fellow, I've created a tray that has one tilted tile edge exposed on each edge of the tray, thereby avoiding violating the islanders' taboos.

Your first challenge in solving this puzzle is simply to lay all twelve pieces flat in the tray; there are 250 ways to do that, and it's not very difficult if you just have a bit of patience. You'll find, though, that almost every such packing has at least one blemish (as least from the point of view of ancient Easter Island culture): there will either be (a) a straight-line crack all the way across or down the puzzle, or (b) a subset of the pieces that form a perfect rectangle or square, or (c) both!

There are just 83 ways to pack the pieces without a straight-line crack, and only six ways to do so without forming a perfect square or rectangle. Your real challenge is to find one of merely three solutions that have neither "blemish". That'll take you a little bit longer to achieve, I think.

Posted by Pavel at 07:53 PM | Permalink | Comments (0)

A week before Thanksgiving, 2006, Kathleen and I drove down to Portland for the weekend, to see some dear friends who'd driven up that far from the Bay Area, and to attend a games party being thrown in their honor (or at least using them as an excuse) by Dave and Diane Perkinson. Dave and Diane are consummate hosts, and they'd invited us to stay in the guest room of their wonderful Craftsman-style house. The bathroom adjoining the guest room still has the great original tile, consisting of squares that have had one of their edges tilted, half one way and half the other. The tiles are laid in straight rows with the tilt of the edges alternating back and forth across the floor, making a kind of angular sine-wave pattern.

At some point as I was sitting in the bathroom, contemplating the world around me, I started to wonder how many ways there were to select three adjacent tiles from the floor in an L shape. (Now, their floor had the sine-wave lines from one row out of phase with those from the next row, but I allowed for both in-phase and out-of-phase patterns in my wondering.) Assuming that, like the real tiles, you couldn't flip a piece over to get its mirror image, I was pleased to discover that there are exactly twelve possibilities. Twelve pieces, times 3 tiles per piece, makes 36, a perfect square. This therefore led immediately to the question of whether or not a complete set of the pieces could be assembled to fill a six-by-six square. I resolved to find out as soon as I returned home, using my packing-puzzle design program.

Once I'd enhanced the software to support pieces that can't be flipped over, I was saddened to discover that the perfect six-by-six square is not, in fact, solvable. Happily, though, a complete set of pieces will nicely fill a variant of the square that has in-phase sine-wave lines at top and bottom. There are two distinct solutions, plus their mirror images. The "Perkinson Guest Bathroom Tile" puzzle is non-trivial to solve, but not wildly difficult either.

Posted by Pavel at 07:51 PM | Permalink | Comments (0)

In the fall of 2004, I was playing around with a deceptively simple little tray puzzle designed by Stewart Coffin and called Four Sleazy Pieces. The eponymous pieces are polyominoes with between five and seven squares each, and the tray is a perfect square whose size is not an integral number of units; it's about 5.8 units on a side. I won't spoil Coffin's fine puzzle here, but suffice to say that, at the time, I hadn't solved it very recently so I'd temporarily forgotten just how "sleazy" the solution is.

While failing to solve it, I stumbled across an interesting property of such a puzzle, and I was excited to note that what I'd found was probably a good psychological "blind spot". These blind spots usually take the form of an assumption most people make that's so "obvious" that it's never questioned, even though it isn't in fact true. Armed with such a blind spot, you can often create a puzzle to exploit it, a puzzle whose solution violates that implicit assumption. That kind of a puzzle has a very pleasant "ah-ha" feeling to it; once you've solved it, you can't figure out how it could possibly have taken you so long.

My resulting puzzle, Sleazier, has that property, and I'm inordinately pleased with it: I think that it's probably the best puzzle I've yet designed. I presented it in the 2005 IPP Exchange, in Helsinki, and it's gotten great feedback in the years since then.

Like Coffin's puzzle, Sleazier has four polyomino pieces ranging from five to seven squares each, and a square tray of a suspiciously odd size; your goal is simply to fit all four pieces flat in the tray. I won't say why, here, but when you compare the "trick" of my puzzle to that of Coffin's, mine definitely deserves its name.

Update: Sleazier is now also available in this economical CD jewel-case edition! (Note: your tray and piece colors are likely to differ from what's shown in this photo. We use a wide variety of colors and every puzzle is made from a different pleasing assortment.)

Posted by Pavel at 07:49 PM | Permalink | Comments (3)

In my very first IPP Exchange, in 2000, I presented a puzzle designed by Bill Darrah, called Raft 5. It consisted of 10 sticks, each with a dovetail notch cut across it and a matching dovetail tab glued on along it. There were five different positions on the stick where a notch or tab could be located, for a total of 10 different pieces, and the puzzle contained one of each. Somewhat surprisingly, it's actually possible to assemble these 10 pieces in a raft-like arrangement, with five sticks going one way laid across five going at a right angle.

Raft 5 is a good puzzle, and for the 2003 Exchange in Chicago, I decided to take inspiration from it. The raft is essentially two dimensional, and I wanted to somehow extend the idea into 3-D. To keep the number of possible pieces down, I made my sticks shorter, with only three positions where a notch or tab could be placed, but I also made the sticks square in cross-section (as opposed to rectangular, as in the raft). This allowed tabs and notches to appear on different sides of the stick, even at right angles to one another.

If you leave out the cases where a notch and tab appear in the same position along the stick (unless they're on opposite sides of the stick), then you get a total of 14 possible pieces. That seemed like too many for a good puzzle, so I picked just half of them; I was perversely tickled by the idea of using seven pieces in an interlocking puzzle, instead of the traditional six. Of course, seven pieces can't make a very symmetric shape, but I made a virtue of that, and designed the puzzle so that the final shape isn't particularly important. Instead, the goal is simply to arrange the pieces so that every piece's tab is inserted into some other piece's notch; that forms the pieces into a kind of folded-up loop, each inserted into the next, like a snake eating its own tail.

There are four solutions to the puzzle, two of which have the fun property that the resulting assembly will balance nicely on the end of one of the sticks. Those two solutions look a bit like a figure standing on one foot, which I like quite a lot; at some point, I want to make a very large set of the pieces to use as a bit of artwork for our yard.

Update (2019):

After being sold out for many years, the Devil's Half Doven is finally available again! I am delighted to bring this design back to life, now in 3-D printed form! The original design is lovingly preserved, and now it's joined by a completely new, smaller relative, the Devil's Mini Doven! This new design uses five of the 14 possible pieces that weren't included in the original version, and has just two solutions. It's definitely a bit easier than its original cousin, but still puts up a nice little fight. In particular, interestingly, most people who succeed in finding one solution seem to have a really hard time finding the other one! Will you be the exception? (If you combine these two puzzles, it might be possible to assemble all 12 pieces. Please let me know if you manage this feat, and send a photo!)

Posted by Pavel at 07:40 PM | Permalink | Comments (2)

For the 2002 puzzle party in Antwerp, I wanted to design something that would lead people to explore the strange world of Penrose's non-periodic kite-and-dart tiles. Some years earlier, someone else had already exchanged a Penrose-based puzzle; that one was just a set of kites and darts that had been distorted a bit to resemble two kinds of birds (and to enforce the normal edge-matching rules). The goal had been simply to fit them together to make the classic regular decagon that crops up every you look in any tiling.

For my own puzzle, I wanted to challenge you to do more than simply learn how to tile the pieces; I wanted it to be a real puzzle. I played around with a Penrose tiling applet for a while and came up with an outline that looked, to me anyway, a lot like the head of a man wearing a turban. That shape required 76 tiles to make, so I broke it up into a set of 16 multi-tile pieces, each containing between 3 and 5 tiles. I then laser cut and etched those pieces with Conway's beautiful curves that show where the legal edge matches are. The resulting puzzle has a unique solution and is fairly difficult.

To make it a bit easier, I added a little removable panel that reveals where some of the tile boundaries are (and that shows why I thought the shape looked like a Grand Vizier). I also included in the package a "little bit bigger hint" that shows where all of the tile boundaries are (but not the piece boundaries, of course).

Finally, I discovered that a subset of pieces I'd chosen could be assembled to form that same classic decagon I mentioned above, so I made the puzzle tray two sided, with the outline of the Grand Vizier on the front and the outline of the decagon on the back. Oddly enough, even though I don't tell you which subset of the pieces you have to use in filling the decagon tray, that side is definitely easier than the front.

Posted by Pavel at 12:40 AM | Permalink | Comments (0)

In 2001, the 21st annual International Puzzle Party was held in Tokyo, and I decided to honor the hosts with a puzzle based on the simple, elegant design of the Japanese flag, also known as Hinomaru (literally, "the circle of the sun"). To start, I drew the flag's design on a 6-by-4 rectangle and then broke it up into twelve 1-by-2 dominoes. Then, to make things tricky, I also colored the backs of all of the dominoes in ways that make them look like potential fronts. Thus, all of the dominoes are double-sided, and it's not at all obvious which side is the front! Add to this the high degree of symmetry in the flag design, which makes the piece placements even more ambiguous, and you have a very difficult puzzle.

(At the 2007 IPP in Australia, six years later, someone came up to me during the Exchange and said, "I spent a long, long time solving that flag puzzle of yours." He then handed me his Exchange puzzle. "This," he said, "is my revenge!" Needless to say, I haven't solved his puzzle yet...)

The Hinomaru puzzle has a unique solution (up to swapping pieces with the same face-up design), and that solution leaves only the front face looking like the flag; the backs of the pieces look entirely random when solved (no helpful hints there!).

I also have an all-paper version of the puzzle, consisting just of the 12 double-sided cards that are sandwiched inside clear acrylic in the version above. This version doesn't come with a tray, just the cards wrapped up in a simple origami envelope.

Posted by Pavel at 11:20 PM | Permalink | Comments (0)

When I was invited to my first International Puzzle Party in 1999, in London, I learned that I would not be allowed to participate in that year's Puzzle Exchange event. There's a very good rule that you need to have attended IPP once before you do the Exchange, to give you a chance to soak up a bit of the party's culture and quality expectations. I decided, though, that I would produce some kind of puzzle anyway, so that I could try to trade it informally for Exchange puzzles (and others).

The only problem was that I had never designed a puzzle before! I mentioned this issue to my friend Barry Hayes and his response was both surprising and surprisingly helpful: "There are puzzles all around us! Almost everything you see is a puzzle; the only tricky part is to recognize how."

As it happened, I was in the local home center the next weekend, buying parts for our garden sprinkler system. Surrounded by all these very uniform pipes and fittings, Barry's words came back to me and I decided that there must be lots of puzzles hidden in these bins. The first thing that came to mind, of course, was a puzzle involving water moving through the pipes, but it didn't take me long to reject that idea in favor of something, anything, less complicated, less "analog". But what else would neatly fill a pipe? Well, anything round would, like ball bearings and dowels...

The result, Pavel's Pipe Dream, is shown at right. There are five dowels, one starting inside each pipe, with notches on the dowels intersecting (and therefore interacting) inside each T fitting. The ball bearing starts just inside the (sealed) endcap in the lower left corner. To solve the puzzle, you must manipulate the dowels through the little windows in the pipes to eventually free the ball. I brought more than 50 copies of the puzzle to London, and succeeded in trading all of them (and the promise of another dozen or so more) to various of the attendees. I came back home after the party drunk with the fact that I'd added something like 65 new puzzles to my collection!

I don't have any more assembled copies of this puzzle left, but I've got lots of copies of the various bits and pieces lying around in the shop. It's not my favorite of my designs, but perhaps if there's sufficient demand I'll produce one more run of them for sale. Leave a comment if you might be interested.

Posted by Pavel at 01:24 AM | Permalink | Comments (0)

After collecting some 90 new puzzles in the IPP 25 puzzle exchange, and maybe another dozen at the puzzle party the next day, you'd think I'd be pretty well saturated with puzzles to play with, and that's true. So what makes this one (additional) new puzzle so cool? Well, there's a story behind that.

Six years ago, I attended my first ever International Puzzle Party, at a hotel near Heathrow Airport in London. (How I finally found out about, and got invited to, IPP is another story.) One of the several great organized excursions that year was a trip to the country manor home of Edward Hordern, who at the time had one of the two or three largest puzzle collections in the world. (Sadly, Edward died less than a year later. Now, the annual puzzle exchange is named in his honor.)

Edward's home, Cane End, was very large and he'd arranged for a huge tent to be set up in the "front yard" to house the tables for lunch and other activities. On each table, there were a few items from his vast collection of something like 25,000 puzzles. A copy of the puzzle shown in the picture, made from water-jet-cut Baltic birch plywood, was one of those. Given the materials and workmanship, it was probably from one of the Finnish contingent.

I couldn't solve it in the brief time I had with it there, so I jotted down the design on the back of a deposit slip from my checkbook, and it sat like that in my wallet for six years. A few months ago, I finally got around to transferring the design into Visio, in preparation for getting it laser cut by my local neighborhood sign maker, but never actually got it done.

Last weekend, at Foo Camp, the folks from Squid Labs had brought both a cutter and some 1/4" Lucite, and they announced Saturday night that they'd be cutting or etching whatever people wanted. I had my laptop with me, and the design was all ready to go, so how could I resist? It was pretty cool watching it do the cutting, seeing a sheet of plastic turn into an interesting puzzle in just a few minutes. Very cool.

I don't know who originally designed this puzzle. If, by chance, you do, please let me know so I can thank them myself. Happily, it turns out to be quite a nice little puzzle.

In case you're interested, my copy of the design appears to the left. The smallest feature size should be equal to the thickness of the material you're using. In my case, it's 1/4" of an inch, which was the thickest acrylic the Squid Labs folks had at the time. For those of you with Microsoft Visio, here's the original design file.

Update on 8/31: More copies of the design file, in DXF format and DWG format. You're welcome, Andy.

Posted by Pavel at 10:50 AM | Permalink | Comments (2)