Pavel's Puzzles

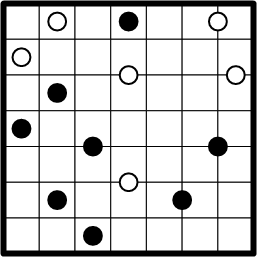This is the example puzzle exactly as presented on the ænigma paper. We are given that we should partition the grid into regions such that (a) each region contains exactly one dot, and (b) the shape of each region is unchanged when rotated 180° around its dot. Each grid square must be included in some region.

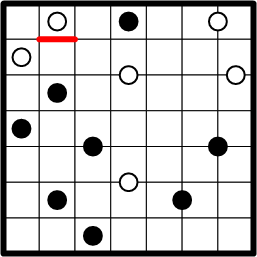We begin by examining the left-most square in the first row that contains a white dot. The boundary of that square's region clearly includes a segment just over the dot (provided by the edge of the whole grid). Each region must be 180° rotationally symmetric around its dot, so we may conclude that this region's boundary also includes a segment just under the dot, drawn here in red.

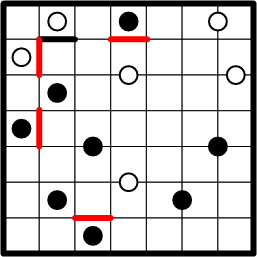Following precisely the same deductive line, applied to other dots at the edge of the grid, we readily obtain four additional boundary segments.

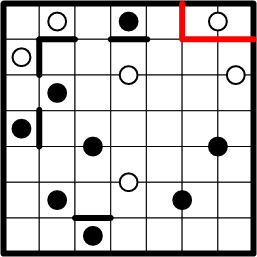The white dot at the right end of the first row straddles the line between two squares, but the same deduction applies: because that region's boundary includes segments just above and to the right of the squares occupied by the dot, symmetry requires that it also include segments immediately below and to the left of those squares.

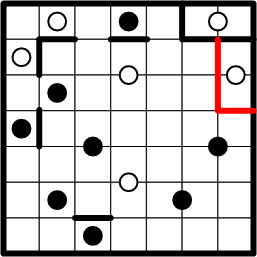Given our previous solving step, we now have the opportunity to apply the very same deduction to the region of the white dot just below, using symmetry to fill in boundary segments and thus completing a second region.

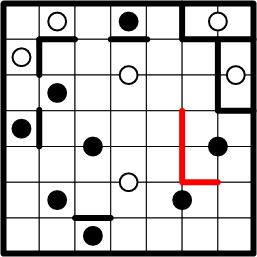The black dot just below where we've been working sits on the intersection shared by four squares, giving the same kind of symmetry-driven deduction a slightly different look. Note that, this time, our technique does not lead to a completed region.

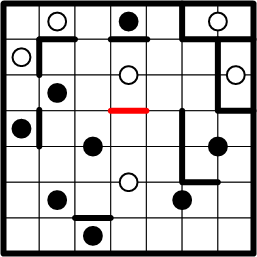Our efforts thus far have, happily, created further opportunities to employ symmetry to fill in additional region-boundary segments. For example, the white dot in the upper centre of the grid now has a boundary segment at the top of the squares it occupies, so we can copy that segment to the bottom of those squares.

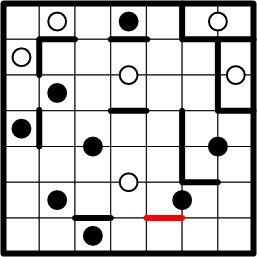Another such opportunity exists for the black dot at the lower right of the grid.

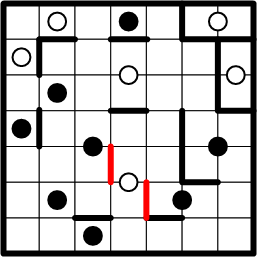The right edge of the pair of squares occupied by that block dot is shared by the pair of squares occupied by the white dot in the centre of the grid. Those two dots mayn't occupy the same region, so we may draw a boundary segment betwixt them. The same reasoning creates a segment between that white dot's squares and those of the black dot just to its left.

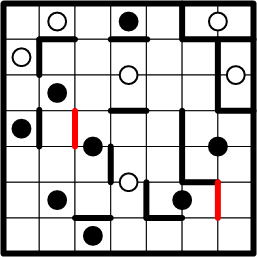Symmetry then allows us to copy segments to the other sides of each of those black dots.

All of our work to this point has entailed only quite straightforward deductions, based on symmetry or shared borders. Sadly, though, there are no further such opportunities available at present, so we must develop new techniques if progress is to continue.

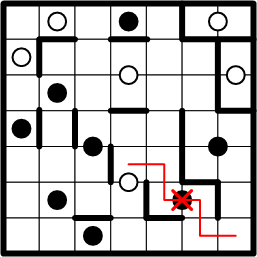We shall proceed by trying to determine that the corner square cannot share a region with any of the other dots reachable from it. As the great Sherlock Holmes is reputed to have said, “When you have eliminated the impossible, whatever remains, however improbable, must be the truth.”

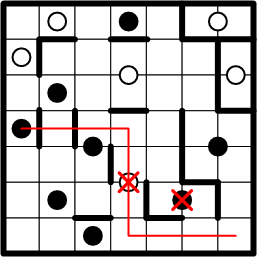We next apply this same technique to try associating our corner square with the centre white dot. Again, there is but one feasible path from the corner to that dot, and again, its symmetric continuation reveals problems. In this case, the path crosses multiple known region-boundary segments and includes multiple squares occupied by other dots. Again, therefore, we may rule out this white dot as the centre of our corner square's region.

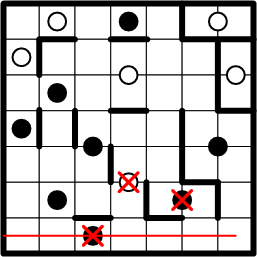Here we apply the same technique to rule out any association of our corner square with the black dot at the bottom of the grid.

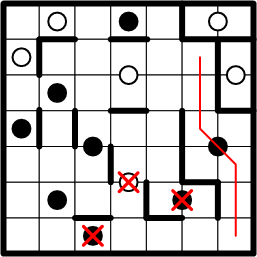Having now ruled out all other possibilities, we are free at last to conclude that our intuitions were correct: the lower-right corner square must, in fact, be part of the region centred around the black dot above it. Again we lightly draw in the path from that square to the dot, along with its symmetric continuation: all of the squares along this path must belong to that dot's region.

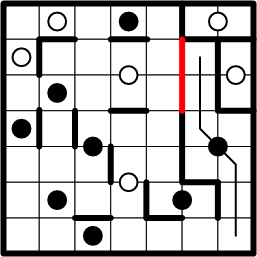Now that the squares along the path have been identified as belonging to the same region, we may return to our original deductive technique, and copy boundary segments according to the dictates of symmetry. Since the bottom two squares have boundary segments to their right (viz., the grid edge), the top two squares must likewise have boundary segments to their left.

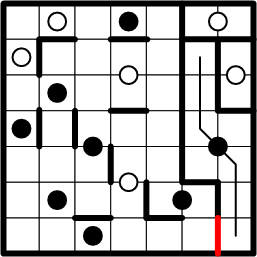Similarly, we may copy another boundary segment from the top of our path to the symmetric position at the bottom, thereby completing our largest region thus far!

The deductive technique just employed, proving that a square may only be legally associated with a single dot, is quite valuable, and very often applicable. Let us next apply it to the second square from the right end of the bottom row, as indicated by the question mark in the diagram.

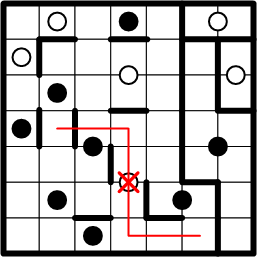First we rule out association with the white dot in the centre of the grid.

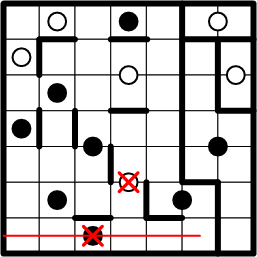Then we do the same for the black dot at the bottom of the grid: here, the symmetric continuation of the path from our subject square cannot even be fully drawn, as it would escape the bounds of the grid!

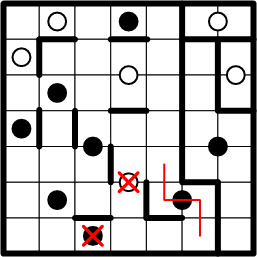Again, having eliminated all other possibilities, we deduce that our subject square must share a region with the black dot above it, and we lightly draw in the corresponding symmetric path.

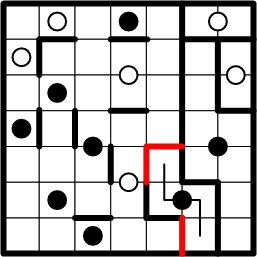And again, we thus enable copying of additional boundary segments to their symmetric positions, once more completing a region.

Flush with these two successes, how could we resist continuing in like fashion, moving our attention one square further to the left?

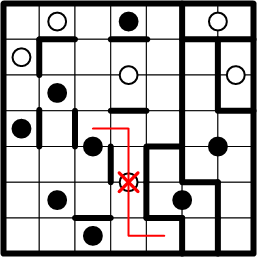Association with the centre white dot is yet again disproven.

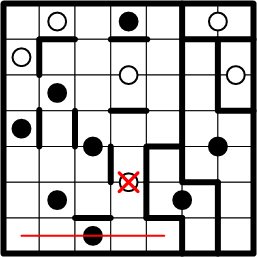This leaves only the black dot at the bottom as a possible centre for our subject square's region, so once again we lightly draw in the path from square to dot, along with its symmetric continuation.

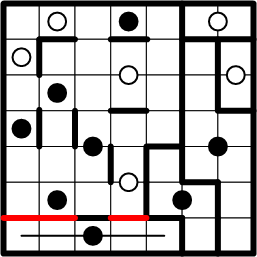Likewise, we once again copy region-boundary segments, according to symmetry, and complete another region.

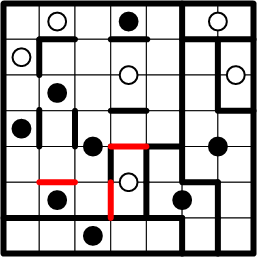All of this furious deductive activity has left us with some catching-up to do in copying boundary segments to their symmetric positions around other dots, including the completion of yet one more region!

In my ænigmas, the individual deductions themselves are often quite straightforward, once identified. The difficulty lies in locating the opportunities for those deductions around the grid. Frequently, I myself must attempt many such deductions, at many sites in the grid, before finally hitting upon one that yields success. I fear that these notes, walking through the solution of the example, may give a false impression, lacking as they do any signs of that search for deductive weaknesses in the conceptual armour of the ænigma. I pray you will not allow yourself to be thus misled.

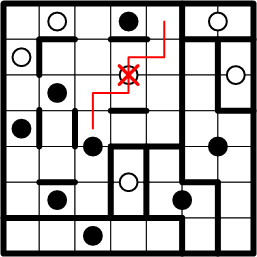First we rule out association with the nearby white dot.

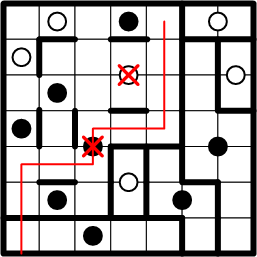Then we turn our attentions to the black dot below that, again encountering the issue where the symmetric continuation of the path from our subject square cannot be fitted within the bounds of the grid.

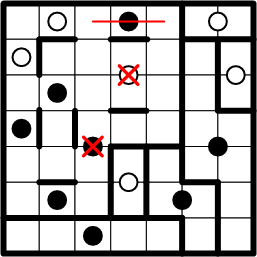That leaves only the nearest black dot for the centre of our subject square's region.

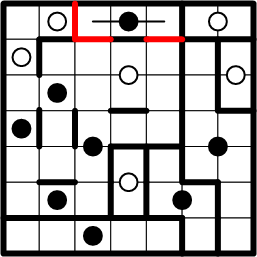We copy adjacent boundary segments to their symmetric positions and thereby complete that region.

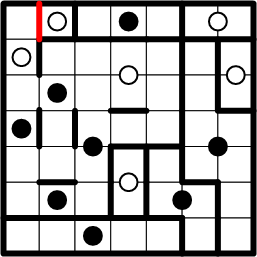That allows more symmetric copying, completing quite a small region indeed!

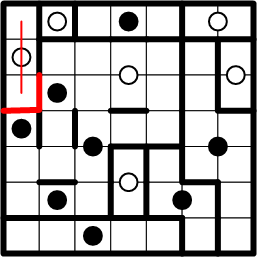The upper-left square can reach only one dot, the white one below it, so this region is quickly completed in now-familiar fashion.

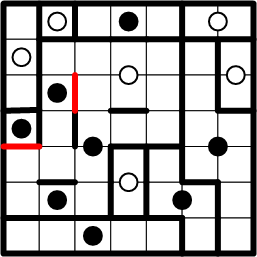Yet more symmetric copying, including yet another completed region.

Although it is possible to continue employing the same deductive technique to make progress at this point (can you see where?), I should like to vary the routine a bit, to illustrate a slight variation. We thus turn our attentions to the square in the very centre of the grid, as indicated.

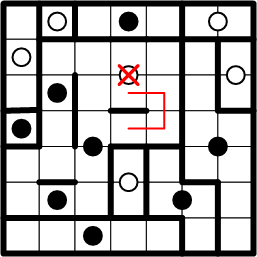That centre square cannot be in the same region as the white dot above it, because that would imply that said region would include squares on both sides of one of boundary segments identified earlier . The very definition of a “boundary” is that it separates regions; it cannot extend into the middle of a single region!

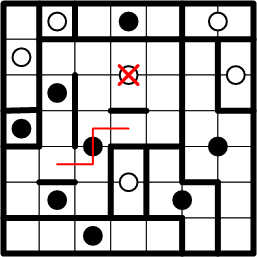That centre square therefore may only be associated with the black dot to its left.

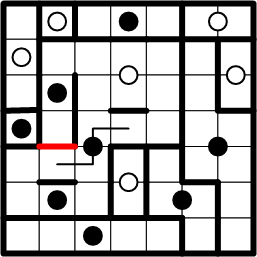Drawing the symmetric path implied by the previous deduction allows us to see a new opportunity for symmetric boundary-segment copying; even though we as yet know comparatively little about the overall shape of this dot's region, we can nonetheless be confident of this much, at least.

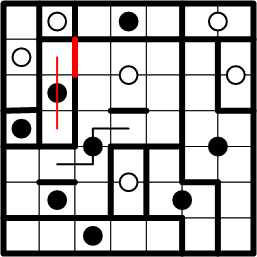As small as the previous step may have seemed, it is sufficient to allow us now to complete another region, using techniques already explained earlier.

Now we return to our prior deductive technique, asking with which dot the indicated square might legally be associated.

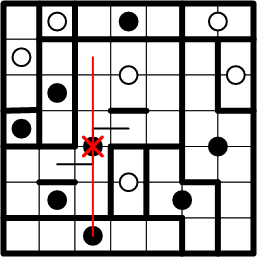We may rule out the black dot below it; the symmetric continuation of the path from our chosen square to the dot extends across a previously determined region boundary.

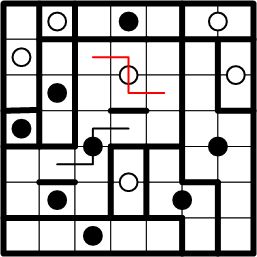That leaves only the nearby white dot as a possible region centre for our chosen square, so we once again lightly draw in the path from square to dot, along with its symmetric continuation.

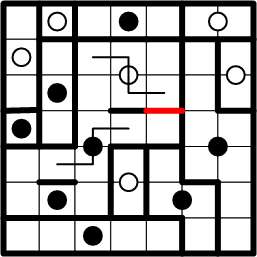That deduction now enables one more segment of symmetric boundary copying.

Consider the indicated square. It is, as it were, hemmed in by the known pieces of the white dot's region. It must, therefore be part of that same region.

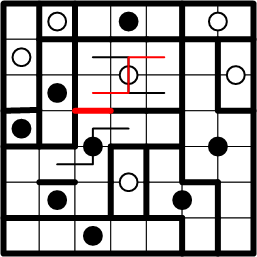That insight allows us to lightly draw another path and then to symmetrically copy one more boundary segment, completing the white dot's region.

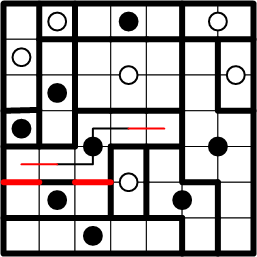We may now see the necessity of extending our notion of the region of the black dot just below the location of the previous step: no other region could include the square just below the right edge of that white dot's region. That knowledge allows us to complete that region and, by exhaustion, the region below it as well!

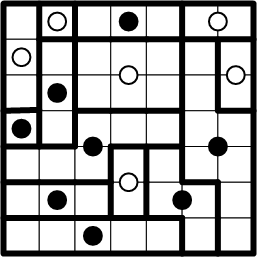Here we pause for just a moment to savor our completed grid. In this diagram, it is easy to see that our deductions have led us to a partitioning that meets all of the requirements in the ænigma rules (which is reassuring), and since we never made any choices, only deductions, we may safely conclude that this solution is unique!

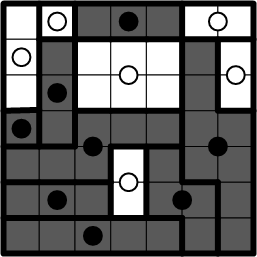We are told to colour each region the same as its centre dot, darkening each black-dot region and leaving the white-dot regions as they are. Following those instructions yields the diagram shown here. If we stand back a modest distance from that diagram and, perhaps, squint meaningfully at it, we can see that it forms a very simple picture of a padlock, so this answer to this ænigma is therefore “LOCK”.