
Adalogical Ænigma #2Walkthrough of the Example PuzzleGreetings, gentle patron!
If you are encountering difficulty making progress on my second ænigma, perhaps you'll find relief in one or both of the following pedagogical aids.
First, concerning the example puzzle shown on the ænigma paper, I've penned a detailed description of how one might go about solving it. That explanation appears below.
Second, if you remain perplexed or frustrated even after perusing that narrative, I have prepared further pages comprising hints on attacking the main ænigma itself. Those pages progress in stepwise fashion, each page revealing only a little more of the solution at a time. You may thus easily read just as far as you require to escape the cognitive quagmire of the moment, without the risk of seeing too much and spoiling what remains of your solving experience.
I trust that these resources will suffice to lift your mental ship off the shoals of perplexity and allow you happily to continue your journey down the river of clarity and deciperment, but if you find that they do not, I invite you to contact my associate, Pavel Curtis, directly for more individualized furtherance.
With my very best wishes for your imminent enlightenment,
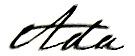
 This is the example puzzle exactly as presented on the ænigma paper. We are given (a) that we should draw one single loop through the centers of squares that enters and leaves each and every boldly outlined region exactly once, (b) within a region containing a number, the loop must pass through exactly that many squares in that region, and (c) if two adjacent squares are in different regions, then the loop must pass through at least one of them.
This is the example puzzle exactly as presented on the ænigma paper. We are given (a) that we should draw one single loop through the centers of squares that enters and leaves each and every boldly outlined region exactly once, (b) within a region containing a number, the loop must pass through exactly that many squares in that region, and (c) if two adjacent squares are in different regions, then the loop must pass through at least one of them.
Are the rules quite clear, then? Jolly good! Let's get started!
 Notice that, up the top-left corner of the grid, there's a region that contains only one square. The loop passes through every region, including that one, and because that square is in the corner, there's only one way for the loop to do that, so we can draw that in.
Notice that, up the top-left corner of the grid, there's a region that contains only one square. The loop passes through every region, including that one, and because that square is in the corner, there's only one way for the loop to do that, so we can draw that in.
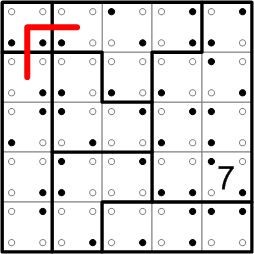
 We can use similar logic in the top-right corner. Of course, the region containing that square is much larger, but it contains a number that's equal to the size of the whole region. Thus, we can deduce that the loop must pass through every single square in that region, including the one in the corner, so again we can draw in a bit of the loop there.
We can use similar logic in the top-right corner. Of course, the region containing that square is much larger, but it contains a number that's equal to the size of the whole region. Thus, we can deduce that the loop must pass through every single square in that region, including the one in the corner, so again we can draw in a bit of the loop there.
 Now we can make use of the rule stating that the loop enters and leaves each region exactly once. The two loop pieces we've drawn so far both intrude on the T-shaped region along the top edge of the grid. That makes one entry and one exit (it doesn't matter which is which, of course), so the aforementioned rule tells us that those two pieces must be directly connected within the region. There's only one way to do that, so we can fill in that connection.
Now we can make use of the rule stating that the loop enters and leaves each region exactly once. The two loop pieces we've drawn so far both intrude on the T-shaped region along the top edge of the grid. That makes one entry and one exit (it doesn't matter which is which, of course), so the aforementioned rule tells us that those two pieces must be directly connected within the region. There's only one way to do that, so we can fill in that connection.
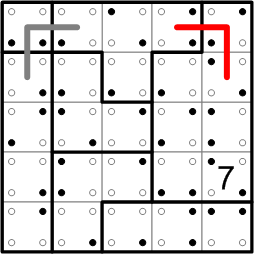
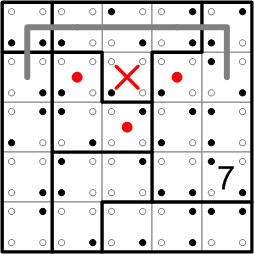 Notice that the loop did not pass through all of the squares in the T-shaped region. Whenever this happens, I mark the skipped-over squares with a big 'X'. These squares are quite important in solving the ænigma: according to the final rule, if an X'ed square has any neighbors that lie in different regions, the loop must pass through those neighbor squares! I always mark such 'required' squares with a big dot; we have three such squares here.
Notice that the loop did not pass through all of the squares in the T-shaped region. Whenever this happens, I mark the skipped-over squares with a big 'X'. These squares are quite important in solving the ænigma: according to the final rule, if an X'ed square has any neighbors that lie in different regions, the loop must pass through those neighbor squares! I always mark such 'required' squares with a big dot; we have three such squares here.
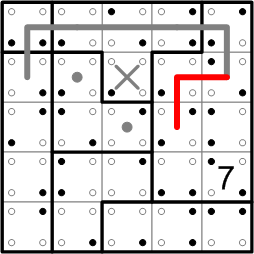 Consider the right-most dotted square. We know that the loop must pass through that square (that's why we dotted it). The loop can't come in from above that square, since it's already passed completely through that upper square, and it can't enter from the square with the 'X', on the left, because that square's already been missed and the loop can't re-enter a region after leaving it. Our dotted square has only two remaining sides for the loop to pass through, so we can confidently fill in a little bit more of its path.
Consider the right-most dotted square. We know that the loop must pass through that square (that's why we dotted it). The loop can't come in from above that square, since it's already passed completely through that upper square, and it can't enter from the square with the 'X', on the left, because that square's already been missed and the loop can't re-enter a region after leaving it. Our dotted square has only two remaining sides for the loop to pass through, so we can confidently fill in a little bit more of its path.
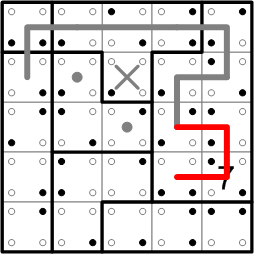 New let's return to the fact that the big seven-square region on the right contains the number '7'. As noted earlier, that means the loop must pass through every single square in that region. At this point, there's only one way left for the loop to do that, keeping in mind that it must then be able to leave the region to continue its journey around the rest of the grid, so we can fill in that path.
New let's return to the fact that the big seven-square region on the right contains the number '7'. As noted earlier, that means the loop must pass through every single square in that region. At this point, there's only one way left for the loop to do that, keeping in mind that it must then be able to leave the region to continue its journey around the rest of the grid, so we can fill in that path.
Note that we don't yet know exactly how the loop will leave this big region, only where it must leave it from.
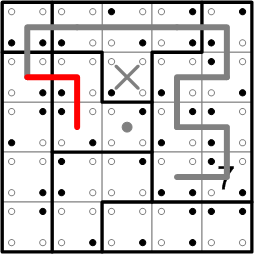 We now turn our attention to the left-most of the dotted squares we introduced earlier. By reasoning that should by now seem quite familiar, we can see that there are only two sides of that square available for use by the loop (and it must pass through that square, recall), so we know two more segments of the loop's path.
We now turn our attention to the left-most of the dotted squares we introduced earlier. By reasoning that should by now seem quite familiar, we can see that there are only two sides of that square available for use by the loop (and it must pass through that square, recall), so we know two more segments of the loop's path.
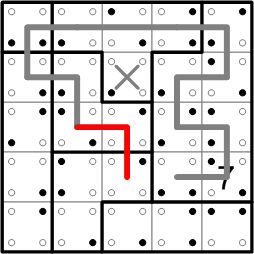 I'm sure I must sound horribly repetitive, but the very same reasoning now applies to the third and final of our dotted squares, allowing us to fill in a bit more of the loop.
I'm sure I must sound horribly repetitive, but the very same reasoning now applies to the third and final of our dotted squares, allowing us to fill in a bit more of the loop.
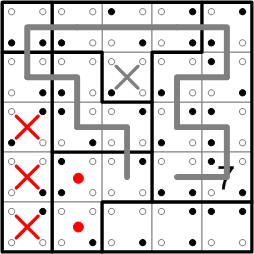 Having now fully dealt with all of the dotted squares from earlier, it seems only fitting to note that the loop has now both entered and exited the tall, straight region on the left edge of the grid, and it did so without passing through three of the region's four squares! That means three more X's for us to enter in those skipped-over squares, and two more neighboring squares from other regions that we can mark with our big dots. More grist for our mill, if you will!
Having now fully dealt with all of the dotted squares from earlier, it seems only fitting to note that the loop has now both entered and exited the tall, straight region on the left edge of the grid, and it did so without passing through three of the region's four squares! That means three more X's for us to enter in those skipped-over squares, and two more neighboring squares from other regions that we can mark with our big dots. More grist for our mill, if you will!
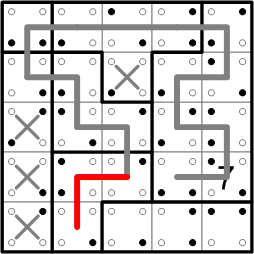 Once more, the reasoning we've used so many times before comes to our aid: the uppermost of the two dotted squares we just introduced can only be passed through by the loop in a single way, so we can fill that in.
Once more, the reasoning we've used so many times before comes to our aid: the uppermost of the two dotted squares we just introduced can only be passed through by the loop in a single way, so we can fill that in.
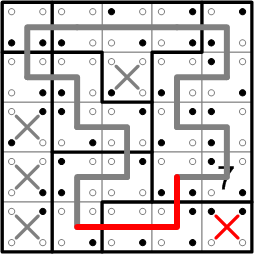 And now, at last, there is only one path remaining for the two ends of our loop to connect, so we may complete our loop-drawing efforts. (Just for neatness, I've also X'd the one final square that the loop has skipped over.)
And now, at last, there is only one path remaining for the two ends of our loop to connect, so we may complete our loop-drawing efforts. (Just for neatness, I've also X'd the one final square that the loop has skipped over.)
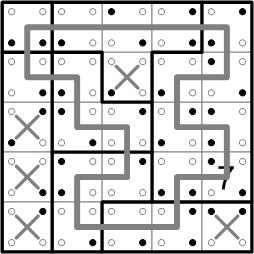 Here's a picture of our completed loop. We may be forgiven, I think, if we pause a moment to appreciate its elegance.
Here's a picture of our completed loop. We may be forgiven, I think, if we pause a moment to appreciate its elegance.
That done, let us now move on to working out the final answer to this ænigma.
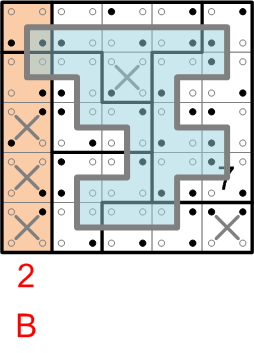 To read off our answer, we must consider each column of the grid in turn, one at a time, looking for little filled-in dots in the corners of the squares, but only those dots that lie on the inside of our elegant loop.
To read off our answer, we must consider each column of the grid in turn, one at a time, looking for little filled-in dots in the corners of the squares, but only those dots that lie on the inside of our elegant loop.
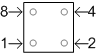 Each filled-in dot has a value, as shown at right, and we are to sum them up in each column.
Each filled-in dot has a value, as shown at right, and we are to sum them up in each column.
I've tinted blue the inside of our loop, and highlighted the first column. With those visual aids, it is easy to see that there's only one relevant filled-in dot in the first column, and it has the value 2, which corresponds to the letter 'B'.
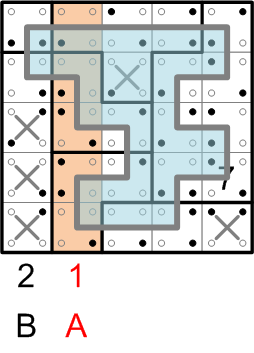 As it happens, the second column likewise contains only one filled-in dot that lies inside the loop, this time with the value 1, representing the letter 'A'.
As it happens, the second column likewise contains only one filled-in dot that lies inside the loop, this time with the value 1, representing the letter 'A'.
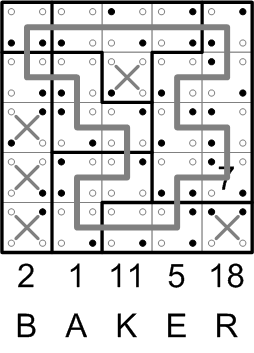 Carefully summing up the values of the relevant dots in each of the remaining columns slowly but surely allows us to read off the final answer to this example ænigma, the word 'BAKER'. (Hmm, I am suddenly wondering what delights the Ada's bookshop café might have prepared today...)
Carefully summing up the values of the relevant dots in each of the remaining columns slowly but surely allows us to read off the final answer to this example ænigma, the word 'BAKER'. (Hmm, I am suddenly wondering what delights the Ada's bookshop café might have prepared today...)
Bravo, we've done it! Now return to your efforts on the original ænigma!
|
Shopping Cart |