Adalogical Ænigma #1

Walkthrough of the Example Puzzle

Greetings, gentle patron!
If you are encountering difficulty making progress on my first ænigma, perhaps you'll find relief in the following detailed description of how one might go about solving the example puzzle shown on the ænigma paper.
With my very best wishes for your imminent enlightenment,
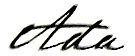
This is the example puzzle exactly as presented on the ænigma paper. We are given that we should draw walls to partition the grid into five regions, each of which contains all of (and only) the letters in the word “MOCHA”. It is terribly important to keep in mind, though: the letters in each region will not necessarily appear in proper reading order!
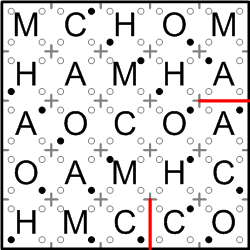Note first the two adjacent squares both labelled “A”, along the right-hand edge of the grid. Since the word “MOCHA” contains only one “A”, these two squares cannot share the same region. That is, there must be a wall separating them. Similarly, a wall must separate the two squares along the bottom edge of the grid that are both labelled “C”.
Next, consider the rightmost square labelled “C” along the bottom edge of the grid. That square might or might not share a region with the square next to it labelled “O”; we don't know as yet. Even if it were to do so, however, that hypothetical region could not also be shared by the square above the “O”, which is also labelled “C”; that would make two squares in the same region labelled “C”.
Thus, whether or not our original “C” is connected to the “O”, the region containing that “C” must extend upward to include the square labelled “H”. I shall notate that bit of learning here by drawing a short line connecting our original “C” to the “H” above it.
I call this solving technique we've just used squeezing, because the region containing our original “C” is being squeezed by its circumstances out of its little corner, in the only direction it can go. Squeezing is a frightfully useful technique that will prove handy over and again in what follows.
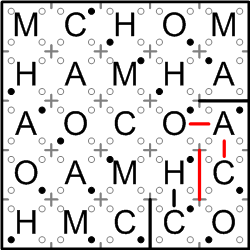Now that we know that that “H” is in the same region as the “C” below it, we can conclude that the “H” cannot be in the same region as the “C” to its right, so we can draw in a wall between them.
It then becomes clear that the region containing that “C” must squeeze out of its corner, connecting the “C” to its neighboring “A” and “O”.
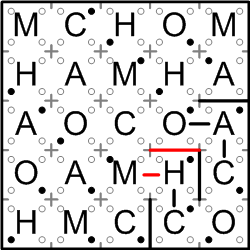The “H” from the previous step still can't share a region with the “C” to its right, so there must be a wall between the “H” and the “O” above it (since that “O” is in the same region as the aforementioned “C”).
Then we see that the region containing the “H” has only one direction remaining in which it can continue squeezing out, so we connect the “H” with the “M” to its left.
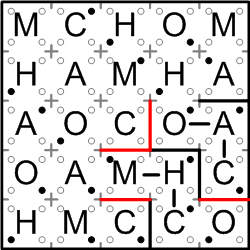Many more walls may now be added to our grid. First, the “C” on the right edge is at last known not to connect to the “O” below it, since that “C” is already connected to a different “O”. Symmetrically, that different “O” cannot connect with the “C” to its left. Finally, by analogous reasoning, the “M” from the previous step cannot connect to either the “C” above it or the one below it.
Excitingly, we can now finish off our very first completed region! The region containing the “M” from the previous step must obviously squeeze out to include the “A” to the left, giving us all five letters of “MOCHA”, so we can draw in the remaining walls to fully enclose our brilliant new region.
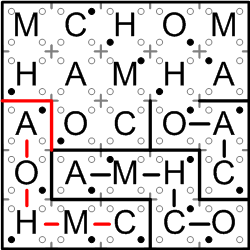From here on out, things progress rather more quickly! The region containing the leftmost “C” on the bottom edge of the grid squeezes out along a single path, instantly giving us our second completed region.
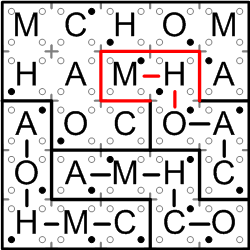Our third completed region follows almost as trivially: it must squeeze out to include the “H”, after which it lacks only an “M”, and there is only the one “M” on offer to round out the region.
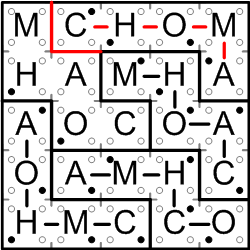Now the region containing the upper “A” on the right edge of the grid squeezes out completely, and the fifth and final region must comprise the squares that remain. We've done it!
Now that we've completed the logic puzzle, it remains only to read off the final answer. For clarity, I've now erased all of the little connecting marks we made earlier.
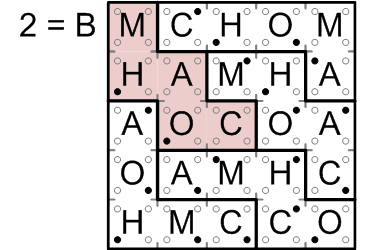We begin reading out the answer by considering each region in turn, left-to-right and top-to-bottom. Obviously, the top-most, left-most region is the one containing the “M” in the upper left corner of the grid. For each square in the region, we convert each filled-in dot into its binary bit value, using the little diagram reproduced at right, and then sum up those values.
There are only two filled-in dots within this region, and they both have value one, for a sum of two. The second letter of the alphabet is “B”, so we note that down.
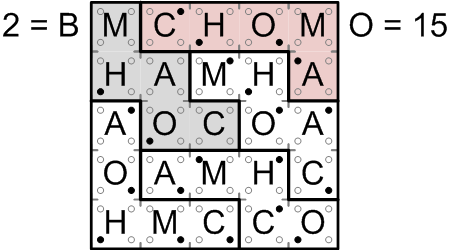The next region across has four filled-in bits, one of each value, for a total of fifteen, giving us the letter “O”.
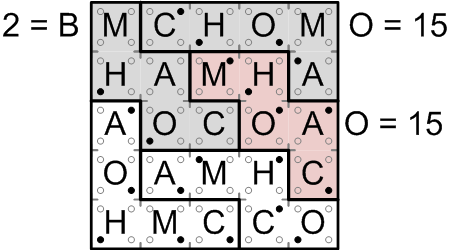By shading in each region as we sum up its binary bits, we can always easily see which region comes next.
With the last two regions summed up, we have all of our answer letters. Reading them in order yields our marvelously apropos final answer, “BOOKS”.
Bravo! Now return to your efforts on the original ænigma!